Définitions
Définition
Un réseau est un graphe (simple) orienté $G=(V, E)$ avec :
- une capacité $c : E \rightarrow \mathbb{R}^{+\star}$ (réels strictement positifs)
- deux sommets spéciaux nommées source (noté $s$) et puits (noté $p$).
exemple de réseau :
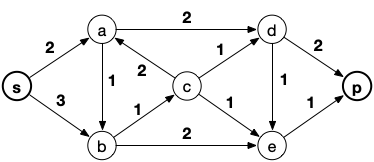
Notez que si on veut une capacité nulle, il suffit de supprimer l'arc
Définition
Un flot dans un réseau donné est une application $f : E \rightarrow \mathbb{R}^{+}$ telle que :
- $0 \leq f(u) \leq c(u)$ pour tout arc $u \in E$
- pour tout sommet $x$ différent de $s$ et $p$, il y a conservation du flot, c'est à dire que le flot entrant est égal au flot sortant : $\sum_{y \in N^-(x)} f(yx) = \sum_{y \in N^+(x)} f(xy)$.
On dit que pour un arc donné $u$ son flux est $f(u)$.
Exemple de flot (nombres en bleu) :
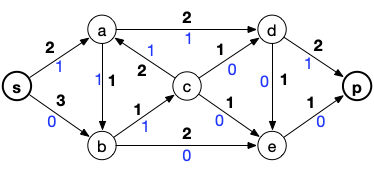
On peut d'ores et déjà noter qu'il existe toujours un flot dans n'importe quel réseau, le flot nul qui vaut $0$ pour tout arc.
Définition
Une coupe est déterminée à partir d'un ensemble $S \subseteq V$ contenant $s$ et pas $p$. En notant $\overline{S} = V \backslash S$ le complémentaire de $S$, une coupe, notée $(S, \overline{S})$ est l'ensemble des arcs ayant leurs origines dans $S$ et leurs extrémités dans $\overline{S}$.
Notez bien qu'une coupe $S$ n'est pas forcément connexe dans $G$. Exemples de coupes pour notre réseau :
- $(\{s\}, V \backslash \{s\})$ qui contient les arcs : $sa$ et $sb$
- $(V \backslash \{p\}, \{p\})$ qui contient les arcs $dp$ et $ep$
- $(\{s, d\}, \overline{\{s, d\}})$ qui contient les arcs : $sa$, $sb$, $dp$ et $de$
Définition
La capacité d'une coupe $c(S, \overline{S})$ est la somme des capacités des arcs de la coupe :
$$c(S, \overline{S}) = \sum_{xy \in (S, \overline{S})}c(xy)$$
On note également pour une coupe $(S, \overline{S})$ les valeurs suivantes :
- $f(S, \overline{S})$ comme étant la somme des flux des arcs ayant pour origine $S$ et pour extrémité $\overline{S}$ (les éléments de la coupe)
- $f(\overline{S}, S)$ comme étant la somme des flux des arcs ayant pour extrémité $S$ et pour origine $\overline{S}$
Exemples :
- $f(\{s\}, \overline{\{s\}}) = 1 + 0 = 1$
- $f(\{p\}, V \backslash \{p\}) = 1 + 0 = 1$
- $f(\{s, d\}, \overline{\{s, d\}}) = 1 + 0 + 1 + 0 = 2$
Valeur d'un flot
On va prouver que pour toute coupe $(\overline{S}, S)$, la quantité suivante est constante :
$$ f(S, \overline{S}) - f(\overline{S}, S) = \mbox{val}(f) $$
Pour tout sommet $x$ de $S$ différent de $s$, on a conservation du flot donc :
$$\sum_{x \in S} (\sum_{xy \in E} f(xy) - \sum_{yx \in E} f(yx)) = \sum_{sy \in E} f(sy) - \sum_{ys \in E} f(ys) = f({s}, \overline{{s}}) - f(\overline{{s}}, {s})$$
De plus, les arcs internes à $S$ sont comptés deux fois une fois pour l'origine de façon positive et une fois pour l'extrémité de façon négative. Les seuls arcs qui ne sont comptés qu'une fois sont ceux qui rentre ou qui sortent de $S$. de là :
$$\sum_{x \in S} (\sum_{xy \in E} f(xy) - \sum_{yx \in E} f(yx)) = f(S, \overline{S}) - f(\overline{S}, S)$$
On en conclut donc que $f(S, \overline{S}) - f(\overline{S}, S)$ est une constante pour n'importe quelle coupe et vaut :
$$ \mbox{val}(f) = \sum*{sx \in E}f(sx) - \sum*{xs \in E}f(xs) = \sum*{xp \in E}f(xp) - \sum*{px \in E}f(px)$$
Ce qui rentre dans le réseau en ressort.
Pour notre exemple, on a donc une valeur de flot de $\mbox{val}(f) = 1$
Flot maximum
On a clairement que :
- $\mbox{val}(f) \leq c(S, \overline{S})$ pour toute coupe du réseau.
- si $\mbox{val}(f) = c(S^\star, \overline{S^\star})$ alors :
- $S^\star$ est la coupe réalisant le minimum de $c(S, \overline{S})$ pour toute coupe $S$
- $\mbox{val}(f)$ est maximum
- pour tout arc $u$ partant de $S^\star$ pour finir en $\overline{S^\star}$, $f(u) = c(u)$
- pour tout arc $u$ partant de $\overline{S^\star}$ pour finir en $S^\star$, $f(u) = 0$
La réciproque est également vraie et nous allons le prouver. On va prouver :
- que le flot maximum existe
- que le flot maximum est égale à la coupe minium.
Existence du flot maximum
Commençons pas montrer que le flot maximum est atteint.
Soient $G= (V, E)$ et $c$ un réseau donné. Une valuation $f$ des arcs de $G$ peut être vue comme un vecteur de l'espace vectoriel $\mathbb{R}^m$ où $m = \vert E \vert$ que l'on munie d'une norme $\vert\vert . \vert\vert$ . Si cette valuation n'est pas un flot, alors :
- soit une des coordonnées est strictement négative : $f(u) < 0$,
- soit la conservation du flot n'est pas respectée pour au moins un sommet de $G$ : la valeur absolue de la différence vaut $d > 0$.
Il existe alors $\epsilon > 0$ tel que toute valuation $f'$ avec $\vert\vert f - f'\vert\vert \leq \epsilon$ n'est pas non plus un flot (on prend $\epsilon$ plus petit que $f(u) > 0$ et $d > 0$) : l'espace de $\mathbb{R}^m$ où $f$ n'est pas un flot est un ouvert. Donc son complémentaire, l'espace de $\mathbb{R}^m$ où $f$ est un flot, est fermé. Ce fermé est de plus borné puisque les flux ne peuvent dépasser les capacités.
Un fermé borné atteignant ses bornes, on en déduit que $\mbox{val}(f)$ va atteindre ses bornes : il existe bien un flot maximum.
Chaîne augmentante
Pour montrer que le flot maximum est égal à la coupe minimum on va introduire la notion de chaîne augmentante.
Une chaîne $c_0 \dots c_k$ dans un graphe orienté $G=(V, E)$ est une suite de sommets tels que pour tout $0 \leq i < k$, soit $c_ic_{i+1}$ soit $c_{i+1}c_i$ soit un arc du graphe.
On suppose que l'on ait un réseau $G=(V, E)$ avec ses capacités $c$ et un flot $f$. Soit alors $C = c_0\dots c_k$ une chaîne de $s$ à $p$ dans $G$.
Par exemple :
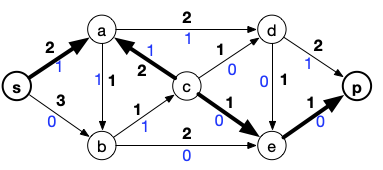
Cette chaîne a 3 arcs qui vont dans le sens de $s$ à $p$ ($sa$, $ce$ et $ep$) et un arc qui va de $p$ vers $s$ ($ca$).
Si l'on peut augmenter la valeurs des arcs allant de $s$ à $p$ et diminuer la valeur des flots allant de $p$ à $s$ on augmentera le flot. Pour garder la conservation des flots, il faut augmenter et diminuer de la même valeur absolue.
Notons alors $C^+$ (respectivement $C^-$) l'ensemble des arcs de la chaîne allant de $s$ à $p$ (respectivement de $p$ à $s$) et calculons :
- $\alpha^+ = \min \{ c(u) - f(u) \vert u \in C^+ \}$
- $\alpha^- = \min \{ f(u) \vert u \in C^- \}$
- $\alpha = \min \{\alpha^+, \alpha^-\}$
Si $\alpha > 0$, $C$ est dit être une chaîne augmentante car on peut augmenter le flot des arcs de $C^+$ de $\alpha$ et diminuer les arcs de $C^-$ de $\alpha$ ce qui garde la conservation du flot et augmente $\mbox{val}(f)$ de $\alpha > 0$.
Dans l'exemple on a : $\alpha^+ = \alpha^- = 1$ : notre flot n'est pas maximum
On en conclut que s'il existe une chaîne augmentante de $s$ à $p$ alors $\mbox{val}(f)$ n'est pas maximum.
Réciproquement, supposons qu'il n'existe pas de chaînes augmentante de $s$ à $p$. Soit alors $S'$ l'ensemble des sommets $x$ tels qu'il existe une chaîne augmentante de $s$ à $x$. L'ensemble $S = S' \cup \{ s\}$ est alors une coupe de notre réseau et :
- pour tout arc $xy$ commençant dans $S$ et finissant dans $\overline{S}$ on a $f(xy) = c(xy)$ sinon il existerait une chaîne augmentante de $s$ à $x$ et de $x$ à $y$, donc une chaîne augmentante entre $s$ et $y$
- pour tout arc $xy$ commençant dans $\overline{S}$ et finissant dans $S$ on a $f(xy) > 0$ sinon il existerait une chaîne augmentante de $s$ à $y$ et de $y$ à $x$, donc une chaîne augmentante entre $s$ et $y$
On en déduit que pour cette coupe : $c(S, \overline{S}) = f(S, \overline{S}) - f(\overline{S}, S)$, la valeur de notre flot est maximum !
On a donc qu'il existe une chaîne augmentante de $s$ à $p$ si et seulement si $\mbox{val}(f)$ n'est pas maximum.
Les arcs d'une chaîne augmentante ne sont pas forcément tous dans le même sens ! La chaîne $sacep$ de l'exemple précédent le prouve. Cette chaîne est augmentante mais les arcs sont $s\rightarrow a \leftarrow c \rightarrow e \rightarrow p$.
Théorème des flots
Finalement :
- il existe une chaîne augmentante de $s$ à $p$ si et seulement si $\mbox{val}(f)$ n'est pas maximum.
- comme le flot maximum est atteint sa valeur ne peut être que la valeur de la coupe minimum puisque l'ensemble des sommets admettant une chaîne augmentante forme alors une coupe.
La coupe minimum est le goulot d'étranglement du réseau.