Arbres de Cayley

Cours/Théorie des graphes/Arbres/Arbres de Cayley

La formule de Cayley donne le nombre d'arbre différents que l'on peut faire à partir d'un ensemble $n$ de sommets donné :

Proposition

Le nombre d'arbre que l'opn peut former avec un ensemble $V$ de $n$ sommets donné est $n^{n-2}$

preuve

Via le code de Prüfer que l'on verra juste après qui est une bijection.

Par exemple, pour les 4 sommets $\{1, 2, 3, 4\}$, il y a 16 arbres différents :

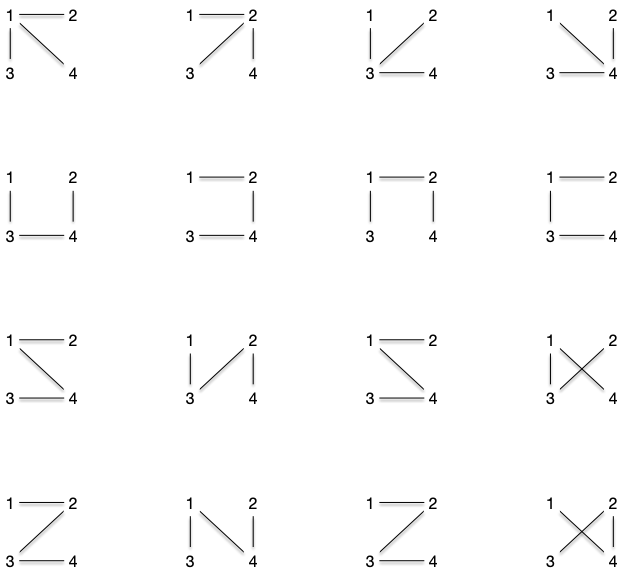
arbres à 4 sommets

Attention, ceci n'est le nombre de formes d'arbres différents à 4 sommets, c'est à dire les différents classes d'équivalences des isomorphismes d'arbres à 4 sommets. Il n'y en a en effet que 2, un chemin et une étoile :

arbres à 4 sommets

Code de Prüfer

Codage de Prüfer

Le codage de Prüfer s'applique à un arbre dont les $n$ sommets peuvent s'ordonner totalement : lorsque les sommets sont des entiers par exemple.

Codage

Code de Prüfer

Soit $T = (V, E)$ un arbre dont les $n$ sommets peuvent être totalement ordonnés. Le code de Prüfer de $T$ est une liste $L$ de $n-2$ sommets construite selon l'algorithme suivant :

L  = []
tant que |V| > 2:
    soit x la plus petite feuille de T et xy son arête
    ajoute y à la fin de L
    supprime x de T

rendre L

En utilisant l'arbre suivant :

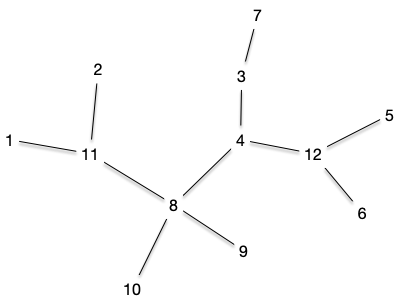
Arbre exemple

Le code de Prüfer est : $[11, 11, 12, 12, 3, 4, 8, 8, 8, 4]$ et correspond à la décomposition suivante :

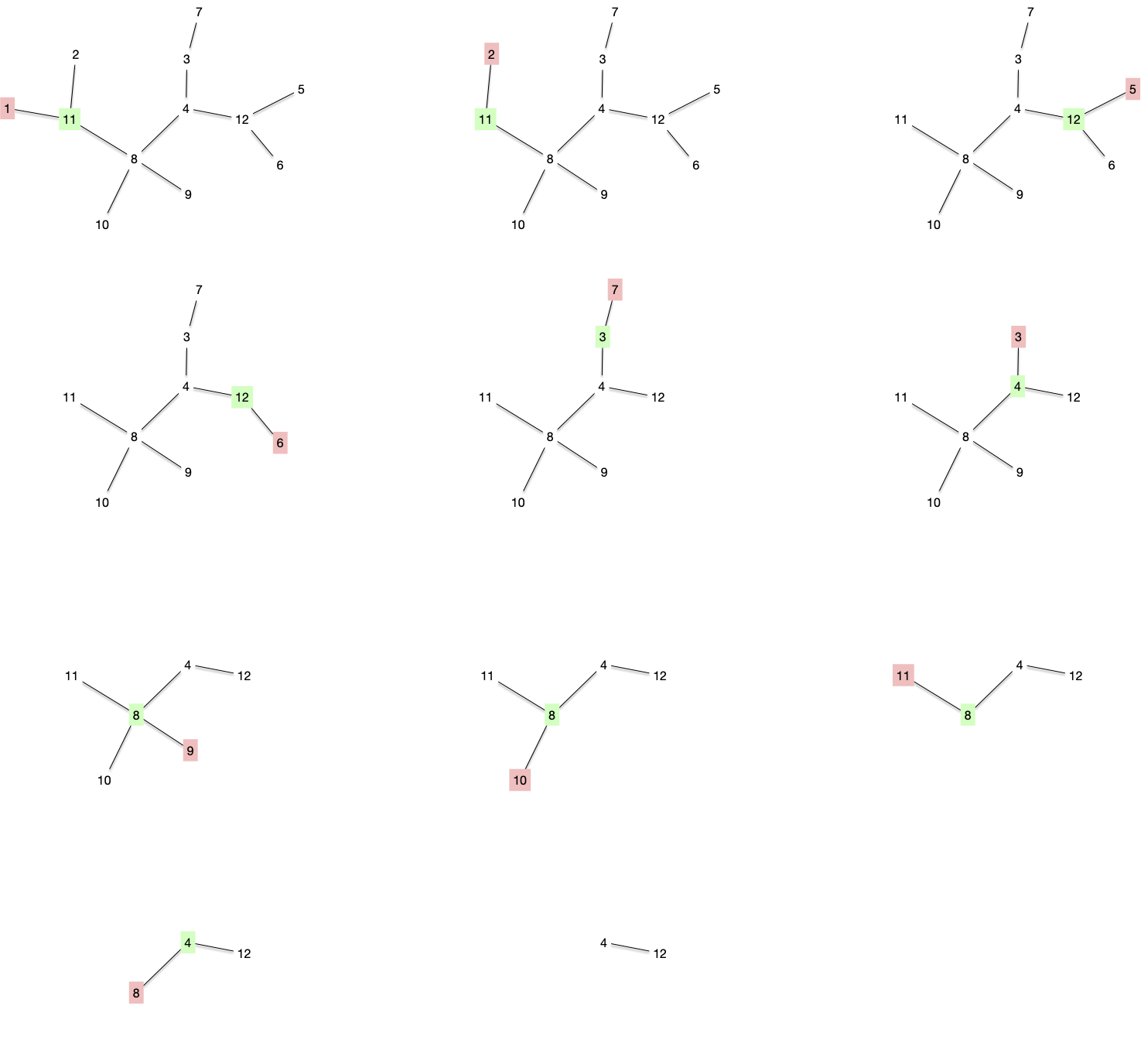
Effeuillage

Notez que par construction on clairement a la propriété suivante :

Proposition

Le code de Prüfer associé à un arbre donné est unique.

preuve

On supprime à chaque fois une feuille d'un arbre, ce qui fait que :

il y a une unique arête à considérer : le sommet $y$ à ajouter à $L$ est unique,
le graphe suivant est toujours un arbre.

De plus :

Proposition

Soit $T = (V, E)$ un arbre dont les $n$ sommets peuvent être totalement ordonnés et $L$ son code de Prüfer associé. Si $x$ est la plus petite de ses feuilles, le code de Prüfer de $T\backslash \{x \}$ vaut $L$ privé de son premier élément.

preuve

Clair.

Enfin :

Proposition

Chaque sommet d'un arbre apparaît un nombre de fois égal à son degré moins 1.

preuve

Comme après chaque itération le graphe considéré est un arbre, on peut facilement prouver la propriété par récurrence. La propriété est évidemment vraie pour un arbre à 2 sommets, supposons la vraie pour un arbre à $n$ sommets. Soit $T = (V, E)$ un arbre à $n+1$ sommets et $x$ la plus petite de ses feuilles et $xy$ son unique arête :

$x$ n'apparaît pas dans $L$
dans $T\backslash \{x \}$, le degré de $y$ est diminué de 1
les sommets de $T\backslash \{x \}$ différent de $y$ ont même degré que dans $T$

Comme le code de Prüfer de $T\backslash \{x \}$ vaut $L$ privé de son premier élément ($y$) et qu'il satisfait l'hypothèse de récurrence :

$y$ apparaît un nombre de fois égal à son degré dans $T$ moins 2 dans le code de $T\backslash \{x \}$ et donc apparaît son degré dans $T$ moins 1 dans le code de $T$
les autres sommets ont même degrés dans $T\backslash \{x \}$ et $T$ et donc apparaissent leurs degrés dans $T$ moins 1 dans le code de $T$.

Décodage

Décodage de Prüfer

$V$ un ensemble de $n$ éléments pouvant être totalement ordonnés. et $L$ une suite de $n-2$ éléments de $V$. On associe un arbre $T=(V, E)$ à $L$ en suivant l'algorithme suivant :

E = ø
tant que L est non vide:
    soit x le plus petit élément de V qui n'est pas dans L
    soit y le premier élément de L
    ajoute l'arête xy à E
    supprime x de V
    supprime le premier élément de L

soient x et y les deux derniers éléments de V
ajoute l'arête xy à E

rendre E

Procédons au décodage de notre code précédent $L=[11, 11, 12, 12, 3, 4, 8, 8, 8, 4]$ pour l'ensemble $V = \{1,\dots, 12\}$

On va obtenir les graphes suivants :

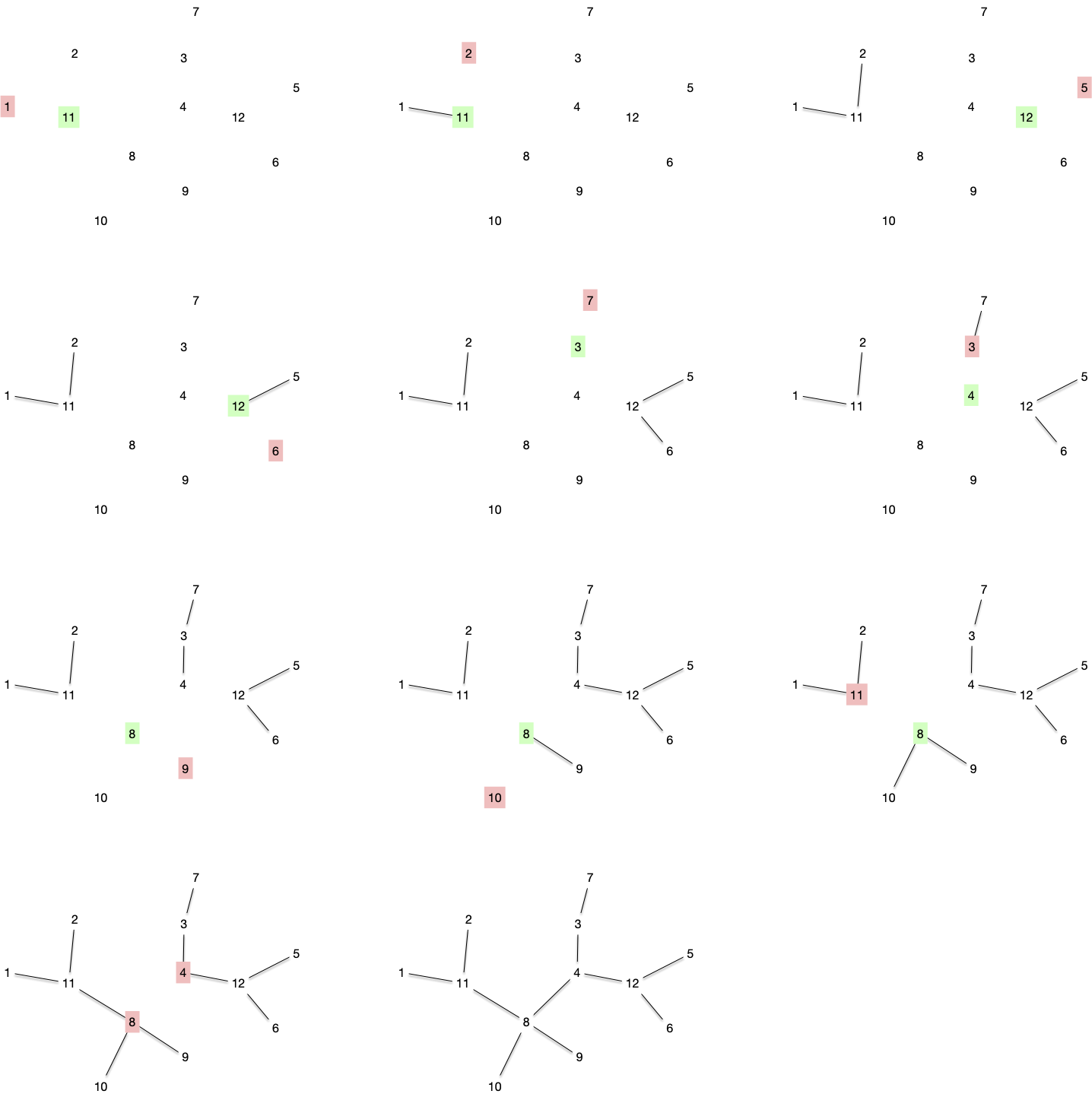
re codage

On retrouve bien l'arbre original ! Mais avant de montrer que ce code est bijectif, montrons déjà que l'on retrouve bien un arbre :

Proposition

Le graphe associé au décodage de $L$ pour l'ensemble $V$ est un arbre

preuve

La propriété est clairement vraie si $V$ possède 2 éléments ($L$ est vide). On suppose la propriété vraie pour un ensemble à $V$ à $n$ éléments et on considère un code $L$ associé à un ensemble $V$ de $n+1$ éléments.

Après la première itération on est face à un un ensemble $V\backslash \{x\}$ et un code $L'$ ($L$ privé de son premier élément) sur lui. Par hypothèse de récurrence, ceci va produire un arbre sur $V\backslash \{x\}$ et comme ajouter une feuille à un arbre reste un arbre, la récurrence est terminée.

Codage et décodage

On peut maintenant terminer cette partie en montrant que codage puis décodage est l'identité.

Proposition

Soit $T = (V, E)$ un arbre dont les $n$ sommets peuvent être totalement ordonnés, $L$ son code de Prüfer associé et $T' = (V, E')$ l'arbre recodé.

On a $T = T'$.

preuve

Il est facile de voir que la première arête recodée est la première arête supprimée en codant. Une récurrence immédiate permet alors de conclure que les deux arbres sont identiques.

Le fait que le codage/recodage de Prüfer soit une bijection montre que le nombre d'arbres que l'on peut créer à partir d'un ensemble $V$ à $n$ éléments correspond au nombre de choix de $n-2$ éléments parmi $n$ avec remise, c'est à dire $n^{n-2}$.

Tirage aléatoire d'un arbre

Trouver un arbre aléatoire d'un ensemble $V$ à $n$ éléments revient à tirer avec remise $n-2$ fois parmi son ensemble de sommets.

On tire aléatoire un arbre à $V$ fixé, pas une forme d'arbre.